POLINOMIAL
Polinomial atau suku banyak adalah pernyataan matematis yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien.
Bentuk umum dari suatu polinomial adalah sebagai berikut
anxn+an-1xn-1+…+a2x2+a1x1+a0
dimana a merupakan koefisien konstan, dan pangkat tertinggi pada polinomial tersebut menandakan orde atau derajatnya, sehingga polinomial diatas memiliki derajat atau orde n.
bentuk umum dari pembagian polinomial adalah
F(x) = B(x) × H(x) + S(x)
Dimana
- F(x) : suku banyak
- H(x) : hasil bagi
- B(x) : pembagi
- S(x) : sisa
metode pembagian polinomial terdapat beberapa cara, diantaranya
1. Metode Pembagian Biasa/bersusun/porogapit
Contohnya adalah jika 2x3 – 3x2 + x + 5 dibagi dengan 2x2 – x – 1
maka hasil bagi = x-1 dan sisa = x+4
2. Metode Horner
Metode ini dipakai untuk pembagi yang berderajat 1 ataupun pembagi berderajat n yang bisa difaktorkan jadi pembagi-pembagi dengan derajat 1.
Jika kita ingin menentukan suatu nilai polinomial dari $f(x)=ax^2 + bx +c$ untuk x = k dengan cara horner, maka dapat disajikan dengan bentuk skema sebagai berikut:
contoh soal:
Hitunglah nilai polinomial untuk nilai x yang diberikan berikut ini.
f(x) =x3 + 2×2 +3x -4 untuk x =5
Jadi nilai polinomial f(x) untuk x =5 adalah 186
Misalkan diketahui
F(x) = 2x3 – 3x2 + x + 5
P(x) = 2x2 – x – 1
Tentukan hasil bagi dan sisanya
Jawab :
F(x) = 2x3 – 3x2 + x + 5
P(x) = 2x2 – x – 1 = (2x + 1)(x – 1)
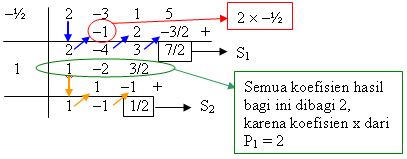
Sehingga p1 : (2x + 1) = 0 -> x = -1/2 dan p2 : (x – 1) = 0 -> x = 1
Kemudian langkah hornernya ditunjukkan pada gambar berikut
Jadi, diperoleh hasil dan sisanya sebagai berikut
H(x) = x-1
S(x) = P1×S2 + S1 = x + 4
Polinomial f(x) ÷ (x – 2) sisanya 24 dan f(x) ÷ (x + 5) sisanya 10. maka f(x) tersebut dibagi  sisanya ialah…
sisanya ialah…
a. x + 34
b. x – 34
c. x + 10
d. 2x + 20
e. 2x – 20
PEMBAHASAN:
Rumusnya adalah P(x) = H(x) . pembagi + (px + q)
Dari soal diketahui:
– f(x) ÷ (x – 2) sisa 24, maka:
f(x) = H(x)(x – 2) + 24
Subtitusikan x = 2, maka:
f(2) = H(2)(2 – 2) + (2p + q)
= 2p + q = 24 …. (i)
– f(x) ÷(x + 5) sisa 10, jadi:
f(x) = H(x)(x + 5) + 10
Dengan Subtitusikan x = -5, jadi:
(f(-5) = H(-5)(-5 + 5) + (-p + q)
= -5p + q = 10 …. (ii)
Eliminasikan persamaan (i) dan (ii):
2p +q =24
-5p +q =10
7p = 14
p =2
Dalam mensubtitusikan p = 2 pada 2p + q = 24
2(2) + q = 24
q = 24 – 4
q = 20
Jika f(x) dibagi  maka:
maka:
sisapx + q = 2x + 20
JAWABAN: D
Contoh No.2
Suku banyak  dibagi oleh x² – x -2 sisanya sama dengan …
a. 16x + 8
b. 16x – 8
c. -8x + 16
d. -8x – 16
e. -8x – 24
dibagi oleh x² – x -2 sisanya sama dengan …
a. 16x + 8
b. 16x – 8
c. -8x + 16
d. -8x – 16
e. -8x – 24
PEMBAHASAN:
Pembaginya adalah: x² – x -2, maka:
 = 0
= 0
(x – 2) (x + 1) = 0
x = 2 dan x = -1
Ingat rumus: P(x) = H(x) + (px + q), maka sisanya (px + q), maka:
– x = 2
f(2) = 2p + q
24 – 3(2)3 – 5(2)2 + 2 – 6 = 2p + q
16 – 24 – 20 + 2 – 6 = 2p + q
-32 = 2p + q … (i)
– x = -1
f(-1) = -p + q
(-1) – 3(-1)3 – 5(-1)2 + (-1) – 6 = -p + q
1 + 4 – 5 – 1 – 6 = -p + q
-8 = -p + q …(ii)
Eliminasikan persamaan (i) dan (ii):
-32 =2p +q
-8 =-p +q
-24 =3p
p = -8
Apabila disubtitusikan p = –p + q = -8
-(-8) + q = -8
q = -16
Maka , sisanya = p + q = -8x – 16
JAWABAN: D
Contoh No.3
Diketahui  dan
dan  adalah faktor dari g(x). Nilai a yang memenuhi adalah …
a. -3
b. -1
c. 1
d. 2
e. 5
adalah faktor dari g(x). Nilai a yang memenuhi adalah …
a. -3
b. -1
c. 1
d. 2
e. 5
PEMBAHASAN:
x2 + x – 6 = 0
(x + 3)(x – 2) = 0
x = -3 dan x = 2
Karena h(x) adalah faktor dari g(x), maka:
– g(-3) = 0

2(-3)3 + a(-3)2 + b(-3) + 6 = 0
-54 + 9a – 3b + 6 = 0
9a – 3b = 48 … (i)
– g(2) = 0

2(2)3 + a(2)2 + b(2) + 6 = 0
16 + 4a + 2b + 6 = 0
4a + 2b = – 22
2a + b = – 11 … (ii)
Eliminasikan persamaan (i) dan (ii):
- 9a -3b 48 | x1 | 9a -3b =48
- 2a +b =-11 | x3 | 6a +3b =-33
JAWABAN: C
Contoh No.4
Jika f(x) dibagi oleh  masing-masing mempunyai sisa 2x + 1 dan 5x + 2 maka f(x) dibagi oleh
masing-masing mempunyai sisa 2x + 1 dan 5x + 2 maka f(x) dibagi oleh  mempunyai sisa…
a. 22x – 39
b. 12x + 19
c. 12x – 19
d. -12x + 29
e. -22x + 49
mempunyai sisa…
a. 22x – 39
b. 12x + 19
c. 12x – 19
d. -12x + 29
e. -22x + 49
PEMBAHASAN:
Misalkan sisa pembagiannya S(x) = px+ q
f(x) dibagi oleh x² – 2x atau x(x -2) → x =2 sisanya 2x + 1, maka:
S(2) = 2x + 1
S(2) = 2(2) + 1
S(2) = 5
2p + q = 5 … (i)
f(x) dibagi oleh x2 – 3x atau x(x – 3) –> x = 3 sisanya 5x + 2, maka:
S(3) = 5x + 2
S(3) = 5(3) + 2
S(3) = 17
3p + q = 17 … (ii)
Eliminasikan (i) dan (ii):
2p + q =5
3p +q =17
-p = -12
p = 12
JAWABAN: C
Contoh No.5
Polinomial ÷ x + 1 sisa 1 dan jika ÷ (x – 2) sisanya 43. Nilai a + b = …
a. -4
b. -2
c. 0
d. 2
e. 4
÷ x + 1 sisa 1 dan jika ÷ (x – 2) sisanya 43. Nilai a + b = …
a. -4
b. -2
c. 0
d. 2
e. 4
PEMBAHASAN:
– Dibagi (x + 1) sisanya 1
maka ketika x = -1, h(-1) = 1

– Dibagi (x – 2) sisanya 43
maka ketika x = 2, h(2) = 43

16 + 20 + 2a + b = 43
2a + b = 43 – 36
2a + b = 7 …. (ii)
Eliminasikan (i) dan (ii):
2a +b =7
-a +b =-2
3a = 9
a =3
Subtitusikan a = 3 dalam 2a + b = 7
2(3) + b = 7
6 + b = 7
b = 1
Jadi a + b = 3 + 1 = 4
JAWABAN: E
Contoh No.6
Salah satu faktor dari (2x³ -5x² – px =3) ialah (x + 1). Faktor yang lain dari suku banyak tersebut adalah…
a. (x – 2) dan (x – 3)
b. (x + 2) dan (2x – 1)
c. (x + 3) dan (x + 2)
d. (2x + 1) dan (x – 2)
e. (2x – 1) dan (x – 3)
PEMBAHASAN:
Yang merupakan faktornya ialah x + 1 –> x = -1
Maka, f(x) = 
= (x + 1)(2×2 – 7x + 3)
= (x + 1)(2x – 1)(x – 3)
Jadi, faktor yang lainnya adalah (2x – 1) dan (x – 3)
JAWABAN: E
Contoh No.7
Ada Duapolinomial  ÷ x + 1 akan mempunyai sisa sama, maka nilai 2m + 5 = …
a. 17
b. 18
c. 24
d. 27
e. 30
÷ x + 1 akan mempunyai sisa sama, maka nilai 2m + 5 = …
a. 17
b. 18
c. 24
d. 27
e. 30
PEMBAHASAN:
Misalkan f(x) = 
Apabila ÷(x + 1 ) –> x = -1 akan memiliki sisa sama,maka:
f(-1) = g(-1)

-1 -4 – 5 + m = 1 – 3 – 2
-10 + m = -4
m = -4 + 10
m = 6
Maka nilai 2m + 5 = 2(6) + 5 = 17
JAWABAN: A
Contoh No.8
Pada f(x) ÷ (x – 1) sisa 3, sedangkan ÷ (x – 2) sisa4. Jika dibagi dengan  maka sisanya ialah…
maka sisanya ialah…
a. –x – 2
b. x + 2
c. x – 2
d. 2x + 1
e. 4x – 1
PEMBAHASAN:
Misalkan sisanya = ax + b, maka
 = (x – 2)(x – 1)
= (x – 2)(x – 1)
Maka sisanya adalah:
f(1) = 3
a + b = 3 … (i)
f(2) = 4
2a + b = 4 … (ii)
Eliminasikan (i) dan (ii):
2a + b =4
a +b = 3
a =1
Dalam Subtitusi a = 1 pada a + b = 3
1 + b = 3
b = 2
Maka sisanya ialah: ax + b = x + 2
JAWABAN: B
Contoh No.9
Banyaknya akar-akar real dari  adalah …
adalah …
a. 2
b. 3
c. 4
d. 5
e. 6
PEMBAHASAN:
x4 -3×3 -3×2 +7x +6 =0
(1 +)(x3 -4×2 +x +6) =0
(x +1)(x+1- x2 – 5x +6) + 0
Sehingga banyak akar- akarnya ada 3
JAWABAN: B
Contoh No.10
Jika polinomia : x3 -4x + px +6 dan z2 +3x -2 dibagi (x + 1) mempunyai sisa yang sama maka nilai p adalah …
a. 7
b. 5
c. 3
d. -5
e. -7
PEMBAHASAN:
Misalkan f(x) = x3 -4×2 + px +6 dan x2 +3x -2
Dibagi (x + 1) maka x = -1
f(-1) = g(-1)


JAWABAN: B
Contoh No.11
Polinomia x2 +ax3 + 2×2 +bx +5jika dibagi (x – 2) tersisa 7, sedangkan suku banyak tersebut dibagi (x + 3) akan memberikan sisa 182. Nilai dari: a2 -4ab +4b2= …
a. 1
b. 4
c. 9
d. 16
e. 25
PEMBAHASAN:
– Dibagi (x – 2) sisa 7, maka:
f(2) = 7

16 + 8a + 8 + 2b + 5 = 7
8a + 2b = -22
4a + b = -11 … (i)
– Dibagi (x + 3) sisanya 182
f(-3) = 182

81 – 27a + 18 – 3b + 5 = 7
-27a – 3b = 78
9a + b = -26 … (ii)
Eliminasikan (i) dan (ii):
9a + b =-26
4a +b = -11
5a = -15
a = -3
Nilai dari : a2 – 4ab + 4b2 = (-3)2 -4(-3)(1)2 =9 +4 =25
JAWABAN: E
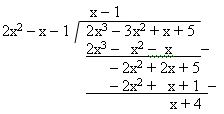






 maka sisanya ialah…
maka sisanya ialah…



Tidak ada komentar:
Posting Komentar